The Wobbly Table Problem, part 2

In part 1 I described the Wobbly Table problem, and explained how a positive solution follows from Dyson’s theorem:

Let g:S2→Rg: S^2 \to \R be a continuous function from the 2-sphere to the real numbers. Then there are two orthogonal diameters of the sphere whose endpoints ±x\pm x and ±y\pm y all take the same value of gg.

In this post I’ll give a proof of Dyson’s theorem. Whereas Dyson’s original proof uses a geometric technique called TT–sets, my proof uses techniques that might be found in a first course in algebraic topology and follows the style of standard proofs of the Borsuk–Ulam theorem.

Let g:S2→Rg: S^2 \to \R be a continuous function from the 2-sphere to the real numbers. We’re interested in the value of gg on 4-tuples of points which are the endpoints of two orthogonal diameters, so we’ll define a function hh, associated with gg, which records the value of gg on four points of a square at once.

Let h:SO(3)→R4h: SO(3) \to \R^4 take the set of 3×33\times 3 orthogonal matrices to Euclidean 4-space, defined as follows:

h([v1,v2,v3])=(g(v1),g(v2),g(−v1),g(−v2))h([v_1, v_2, v_3]) = (g(v_1), g(v_2), g(-v_1), g(-v_2))

Here [v1,v2,v3][v_1, v_2, v_3] is a matrix expressed in terms of its column vectors. The vectors v1,v2,−v1,−v2v_1, v_2, -v_1, -v_2 form the vertices of a square, and hh records the values of gg on this square (see the picture).

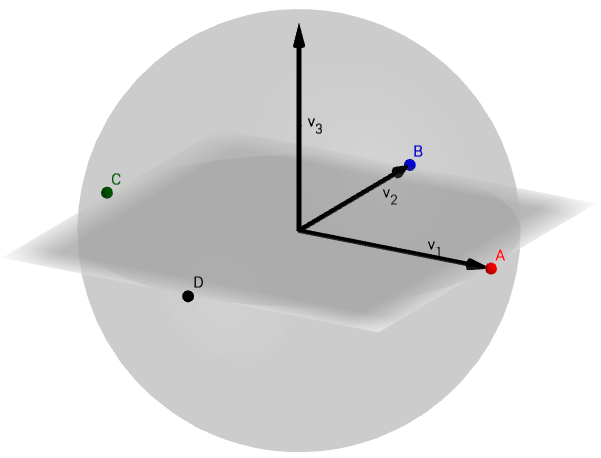
⟶h(g(A),g(B),g(C),g(D))\overset{h}{\longrightarrow} (g({\color{red} A}), g({\color{blue} B}), g({\color{darkgreen} C}), g(D))

Now we make two observations. First, the function hh has symmetry: it’s keeping track of labels on the vertices of the squares, but if we rotate the square, the value of hh on that different square is related to the value of hh on the original square. We express this symmetry as equivariance with respect to a group action, which we now explain.

The group of symmetries of a square is the dihedral group D4D_4 (of order 8). This group has a representation ρ:D4→SO(3)\rho: D_4 \to SO(3) as standard rotation matrices (as the symmetries of a square with vertices at the first two standard basis vectors and their negatives).

The group D4D_4 also acts on R4\R^4 by permuting coordinate factors. Think of the four coordinate factors of R4\R^4 as being labeled by the vertices A,B,C,DA, B, C, D of a square; then, applying a symmetry of a square permutes the labels.

Therefore we can express the equivariance of hh by:

h([v1,v2,v3]⋅ρ(a))=h([v1,v2,v3])⋅a,∀a∈D4.h([v_1, v_2, v_3] \cdot \rho(a)) = h([v_1, v_2, v_3]) \cdot a, \forall a \in D_4.

Second, phrased in terms of hh, Dyson’s theorem is equivalent to saying that the image of hh intersects the diagonal of R4\R^4, △R4={(x,x,x,x):x∈R}\triangle \R^4 = \{ (x,x,x,x) : x \in \R \}. If Dyson’s theorem failed to hold for a given function gg, then the function hh could be deformed so that its image lies in the unit 2-sphere in the 3-space orthogonal to △R4\triangle \R^4. In the picture below, we show the diagonal in R4\R^4 as well as the 2-sphere which lies orthogonal to it. Note that we show a 3-dimensional analogue: we have the diagonal pictured in R3\R^3, with a 1-sphere (a circle) in the complementary 2-plane to the diagonal. In 4 dimensions, there is actually a 2-sphere lying in the complementary 3-space to the diagonal.

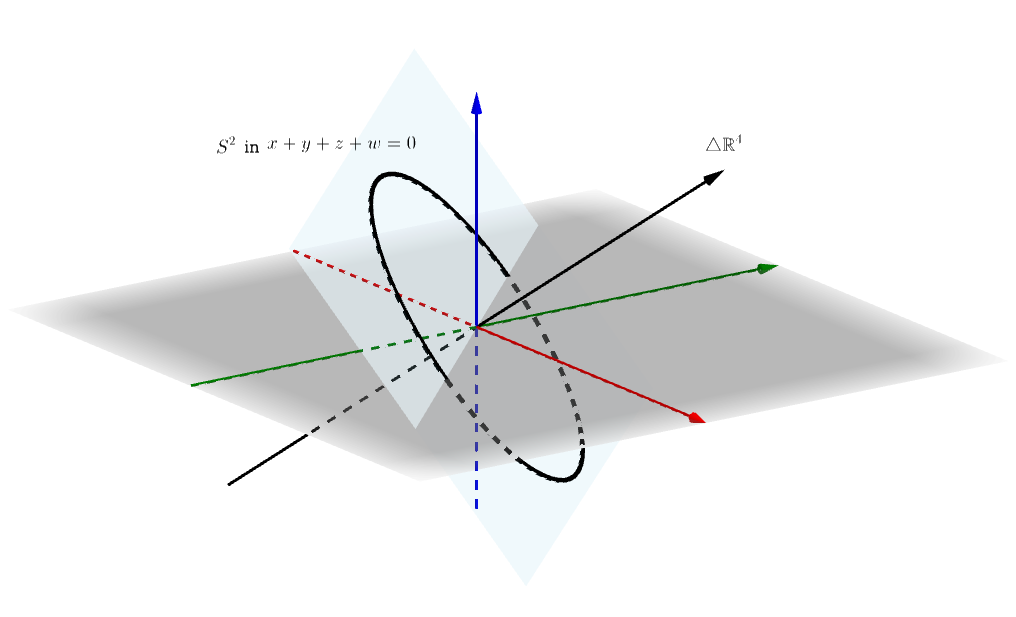
Furthermore, this deformation remains equivariant: now D4D_4 permutes the vertices of a regular tetrahedron in S2S^2 rather than permuting the coordinates in R4\R^4.

After these two observations, Dyson’s theorem will follow from:

There is no D4D_4–equivariant continuous function from SO(3)SO(3) to S2S^2, where the group acts on SO(3)SO(3) by right multiplication and on S2S^2 by permuting the vertices of a regular tetrahedron.

I give the proof of this lemma in part 3.