The Inscribed Rectangle Conjecture: Ideas towards a solution •

This is part 2 of a two-part post. In the first part I described the Inscribed Square and Inscribed Rectangle Conjectures. In this part, I’ll give a quick summary of part 1 so that you don’t need to re-read it, and then I’ll explain some thoughts I’ve had about how to tackle the Inscribed Rectangle Conjecture. While the first part was aimed at a non-technical audience (approximate level: high school geometry), this part contains technical details, approximately at the level of graduate geometry and topology. Feel free to read on! The level of technical detail will gradually rise, so feel free to bail whenever you like.

In part 1, I explained the standard proof strategy for the Inscribed Square Conjecture, that regular enough simple closed curves in the plane have an odd number of inscribed squares: an ellipse has one inscribed square; deforming the ellipse into another curve causes squares to appear and disappear in pairs; therefore the other curve has an odd number of inscribed squares.

I then explained why this strategy doesn’t work for inscribed non-square rectangles with prescribed aspect ratio. Counting non-square rectangles with fixed aspect ratio, an ellipse has two such rectangles; rectangles still appear and disappear two at a time through deformations of the ellipse; therefore some deformation to another curve might (for all we know) cause all rectangles to cancel out.

That’s the essence of the difficulty of the Inscribed Rectangle Conjecture compared with the Inscribed Square Conjecture. What I’ve just given is the very short version of a longer discussion I gave in part 1.

There actually is one small but interesting bit of published progress on the Inscribed Rectangle Conjecture, which I have saved until now to mention. It’s a beautiful mathematical idea (for aesthetic reasons similar to what I discussed in my post on why I was interested in the Wobbly Table puzzle); it inspired my own attempts to try to prove this conjecture; and I haven’t seen anyone else publish any results taking this idea further. (Though for all I know people have privately tried and failed.)

Vaughan’s theorem •

I’d like to elaborate on what this theorem, due to H. E. Vaughan in 1977, does and does not state. First of all, the aspect ratio of the rectangle is not guaranteed. The Inscribed Rectangle Conjecture asks whether simple closed curves have inscribed rectangles of every aspect ratio, and this theorem guarantees only one rectangle of indeterminate aspect ratio (which might be square). Second, quite interestingly, there is no regularity hypothesis. In other words this theorem is valid even for the horrible fractal messes that no one knows how to deal with in the general Inscribed Square/Rectangle Conjectures. That fact makes it quite interesting as a source of potential ideas for how to prove the general conjectures.

Vaughan’s proof is both beautiful (it’s surprising, using a mathematical fact which seems totally unrelated) and also unfortunate, in that it doesn’t seem that the method generalizes easily. Here’s the proof. It relies on the well-known fact that non-orientable surfaces don’t embed in 3–space. (To non-technical readers: the Klein bottle is an example of a non-orientable surface, and if you try to make a physical one, you have to allow it to pass through itself. There are other non-orientable surfaces and they all have this “defect”, though what is a defect from the point of view of physical construction is an advantage to us in the following proof.)

The non-embeddability of the real projective plane is true for arbitrary continuous maps, not just smooth maps, which is why this theorem can get away with not having any regularity assumption. On the other hand, if you’re given an arbitrary map of the real projective plane into 3–space, it’s very difficult to say anything about what its self-intersection set looks like, beyond “non-empty”.

My attempts at solving this problem come from taking Vaughan’s idea, and trying to analyze what the self-intersection set looks like if we assume that the simple closed curve (and hence the mapping of the real projective plane) is smooth, not just continuous.

Self-intersections of a smooth surface in 3–space •

Self-intersections of smooth surfaces in 3–space — as opposed to arbitrary continuous surfaces — are well-studied. See for example J. Scott Carter’s How Surfaces Intersect In Space: An Introduction To Topology. The singular set of a surface in 3–space is generically (ie after a small perturbation) a union of curves of double points (prototypically, the union of the xy-plane and yz-plane), isolated triple points (prototypically, the union of the xy-, yz-, and xz-planes), and isolated branch points. Branch points are also known as “Whitney umbrellas”. Think of pinning together two sheets of paper at a single point, and cutting them simultaneously with a pair of scissors right up to the pin point. Then there are four cut edges all right next to each other. Glue the top left to the bottom right, and the top right to the bottom left. You wind up with a curve of double points ending at the branch point (where the pin is).

If a surface is compact and its singular set when mapped into 3–space is disjoint from its boundary, then the preimage of the singular set in the surface is a union of immersed circles. The map into 3–space, when restricted to this preimage, is a double cover away from the triple and branch points. A union of some combination of: a circle being mapped to a segment with branch point caps via reflection; a circle being mapped to a circle via a degree 2 map; and two circles being mapped each with degree 1 to the same circle.

Self-intersections of Vaughan’s construction •

The surfaces arising from Vaughan’s construction aren’t as fully general as arbitrary smooth maps of a surface into 3–space. The surface is fully determined by the simple closed curve forming its boundary; we might expect to see some restriction on its singular set. And in fact we do. For example, although a general Möbius strip in 3–space with boundary along a simple closed curve might be immersed (have singular set without branch points), it turns out that if it arises from Vaughan’s construction then it has at least two branch points.

Branch points •

Let’s see an example: if we take an ellipse as our simple closed curve, what sort of surface does Vaughan’s construction give? What does its singular set look like? We get a Möbius strip mapped into 3–space; since the ellipse is convex, the midpoint of any secant lies in the interior. That means that Vaughan’s surface for the ellipse is some sort of singular dome lying over the ellipse. What about its singular set? Every diameter of the ellipse (every secant passing through the center) is sent to the singular set of the surface: a secant through the center which is not the major or minor axis always has exactly one partner which has the same length; that means that the diagonal (relative to the major/minor axes) diameters get sent to the double set of the surface. The major and minor axes don’t have partners with the same length and midpoint, but they are limits of secants which do; therefore they get mapped to branch points. Thus the singular set of Vaughan’s surface corresponding to the ellipse consists of a single arc of double points, capped at either end by branch points.

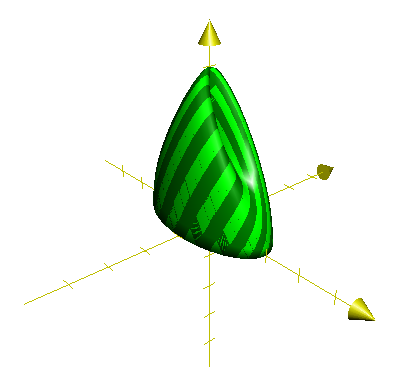
In this example, notice that the branch points occur at critical points of the height function. This is not a coincidence.

In fact we have: A Möbius strip arising from Vaughan’s construction on a generic smooth simple closed curve has branch points precisely at those secants which are orthogonal to the curve at both endpoints. These are precisely the critical points of the height function (ie the function which takes the length of the secant).

Here’s the proof. Parametrize the curve $\gamma : S^1 \to \R^2$ by arc length. To see the second statement, that critical points of the height function are precisely those where the secant is orthogonal to the curve at both endpoints, simply observe that critical points of $z(s, t) = \| \gamma(s) - \gamma(t) \|$ occur at the critical points of $z^2$, and compute

$$(\partial_s z^2, \partial_t z^2) = 2(\gamma'(s)\cdot (\gamma(s) - \gamma(t)), \gamma'(t)\cdot (\gamma(t) - \gamma(s))).$$

Critical points of $z$ are branch points: from the first paragraph, $\gamma'(t)$ and $\gamma'(s)$ either point in the same direction or in opposite directions. If they point the same (resp. opposite) direction, moving the secant in the direction $\partial_s - \partial_t$ (resp. $\partial_s + \partial_t$) preserves the midpoint and length of the secant up to first order, ie is equivalent to spinning the secant about its center without changing length. Therefore the differential of Vaughan’s map fails to be injective, so it fails to be an immersion.

Conversely, at secants which are not orthogonal to the curve at both endpoints: if the tangents to the curve at the endpoints are not parallel, then moving the secant along $\partial_s$ and along $\partial_t$ moves the midpoint in independent directions. If the tangents at the endpoints are parallel, and not orthogonal to the secant itself, then $\partial_s \pm \partial_t$ move the midpoint by a nonzero vector and respectively lengthen and shorten it; therefore moving the secant by independent directions in 3–space. Thus the Vaughan map has injective differential.

That concludes the proof.

Note that branch points come in pairs, so we actually get at least two of them. This proposition is important! The reason it’s important is that in the case of the ellipse, it’s the fact that we have branch points that lets us find a rectangle of every aspect ratio. At one branch point, the major axis splits into a very narrow rectangle; the rectangle opens up and passes through the intermediate square before closing up the other way at the minor axis. If we weren’t guaranteed a pair of branch points, we might not find very narrow rectangles.

Unfortunately it still seems possible that there are rectangles where we don’t find rectangles of every aspect ratio. In the case of the ellipse, the branch point splits into a narrow rectangle which closes up the other way; ie it passes through every aspect ratio. But it can happen for some Vaughan surfaces that there’s a branch point (secant length critical point) which opens up into narrow rectangles and then closes up the same way.

Self-intersection curves without branch points •

Aside from a circle in the Möbius strip mapping to a line segment capped by branch points in 3–space, there are two other kinds of self-intersection curves: one circle in the Möbius strip covering a circle in 3–space by a degree 2 map, and a pair of circles in the strip covering a single circle in 3–space by a pair of degree 1 maps.

I don’t actually know whether these can occur for Vaughan surfaces in general position! The former, if it could actually happen, would look something like the following. Take a circle for our smooth simple closed curve. This is very far from being in general position, because its singular set consists of a curve’s worth of secants (the diameters of the circle) all getting mapped to a single point (midpoint equal to the center of the circle, length equal to twice the radius). Recall that in general position singular points are either branch points, or two-to-one, or three-to-one, not entire-circle-to-one.

But for the sake of illustration: take a single rectangle, say aligned with its long side along the x-axis. Simultaneously rotate it counterclockwise and also fatten its aspect ratio, so that the two diagonals swap places via a counterclockwise rotation at different speeds. This yields a circle’s worth of rectangles, and if the Vaughan surface were perturbed, would look like a circle in the Möbius strip mapped by degree 2 to a circle in 3–space. Note that there is exactly one square in this curve of rectangles, and that not all aspect ratios are represented; the horizontal starting rectangle is the narrowest.

I don’t know how to visualize two circles mapping to a single one, or whether it even occurs in the Vaughan surface for a simple closed curve.

What would a counterexample look like? •

In this section I’ll give some restrictions on the singular set of the Vaughan surface of a generic counterexample to the Inscribed Rectangle Conjecture. A key observation is that the Inscribed Square Conjecture, which is known for smooth simple closed curves, says that such a curve will have an odd number of inscribed squares.

Note that the Vaughan surface in $\R^2 \times \R_{\geq 0}$ can be lifted to $\R^2 \times \R_{\geq 0} \times (\R/\pi\Z)$, where the coordinate of the last circle factor is the angle of the secant modulo $\pi$. (The secant is an unordered pair of points and therefore the angle it makes with the horizontal is well-defined modulo $\pi$.) As an aside, note that the lift of the Vaughan surface is an embedding: two secants have the same midpoint, length, and angle with the horizontal if and only if they have the same endpoints.

Consider a circle of secants in our Möbius strip which gets mapped to the singular set of the Vaughan surface. Parametrize that circle arbitrarily, and take the corresponding “partner” parametrization of its “partner circle”. The partner circle is the circle of secants which makes a rectangle with the first circle. For example, in the case of the ellipse, we could take one circle to be diameters running counterclockwise, parametrized starting at the major axis, and then its partner circle would be (in this case, but not always) that same circle parametrized clockwise.

For a circle mapping to a segment with branch points, it is its own partner and the partner parametrization runs the other way. For a circle mapping by degree 2 to a circle in the Vaughan surface, it is its own partner and the partner parametrization has the same degree and is offset. For two circles mapping by degree 1 to a single circle, they are each other’s partner.

For each circle of secants, we have a well-defined angle difference function, measuring the angle difference in the final coordinate of the lift of the Vaughan surface, between a circle of secants and its partner parametrization.

If we assume our smooth simple closed curve is a counterexample to the Inscribed Rectangle Conjecture, then every angle difference function on circles of secants is non-surjective, and hence has degree zero. For circles mapping by degree 2, this was immediate already, but for circles mapping to segments, and for pairs of circles mapping by degree 1, this adds new information.

In a counterexample, all circles of secants which map to segments capped by branch points, must open and close the same direction. More precisely, such a circle in the Möbius strip, when mapped to the last coordinate in the lift of the Vaughan surface, must have degree zero. Phrased differently, the angles traced out by the secants in this circle have degree 0 in $\R/\pi\Z$. Additionally, since the total number of inscribed squares is odd, there must be an odd number of circles which map by degree 2 to the singular set, since each of those contribute an odd number of inscribed squares. The number of squares contributed by pairs of circles mapping by degree 1 is always even.

Possible future approaches •

To answer whether counterexamples to the Inscribed Rectangle Conjecture exist, I think we’d need to know more about the nature of the singular set of the Vaughan surfaces. Can a Vaughan surface which is in general position have components which are circles, not capped by branch points? My guess is no, but I don’t know how to prove this. Can this be tackled from the point of view of self-intersections of 3–manifolds in 4–space, by looking at an isotopy of an ellipse into an arbitrary smooth simple closed curve? What sorts of self-intersection sets can appear and disappear in this isotopy?

Can a smooth simple closed curve whose Vaughan surface is not in general position, be perturbed so that the new Vaughan surface is in general position? Of course the Vaughan surface could be perturbed to be in general position, but the question is whether that perturbation can be chosen to come from a perturbation of the smooth simple closed curve.

In conclusion… •

That about sums up my current thoughts about this problem. If you have ideas, I’d love to hear them. My contact info is at the top of this page.